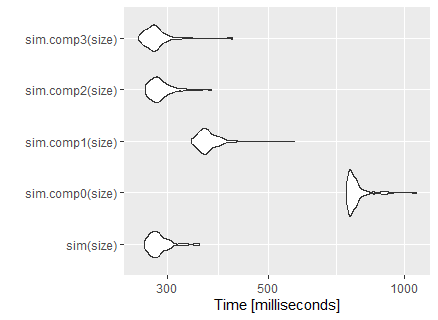
There are some tricks you can follow in order to get a faster code, we will use our Pi function from the previous topic as our baseline:
sim <- function(l) {
c <- rep(0,l); hits <- 0
pow2 <- function(x) { x2 <- sqrt( x[1]*x[1]+x[2]*x[2] ); return(x2) }
for(i in 1:l){
x = runif(2,-1,1)
if( pow2(x) <=1 ){
hits <- hits + 1
}
dens <- hits/i; pi_partial = dens*4; c[i] = pi_partial
}
return(c)
}